Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.
This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)
Find the integral (as far as you can): . Assume that f is a function such that the derivatives and integral are well defined.
A first thought may be to distribute the  , but after that step it is unclear how to proceed! Instead, notice that we have a product of two functions, namely
, but after that step it is unclear how to proceed! Instead, notice that we have a product of two functions, namely 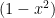 and
and  . This is a good indication that integration by parts would be a helpful approach!
. This is a good indication that integration by parts would be a helpful approach!
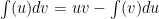
To apply this, we have to decide what and
and  are. Clearly if we take the derivative of f(x) again we will be moving in the wrong direction by making things more complicated. Also, it is really easy to take the derivative of
are. Clearly if we take the derivative of f(x) again we will be moving in the wrong direction by making things more complicated. Also, it is really easy to take the derivative of  which we will have to do with whatever we choose as
which we will have to do with whatever we choose as  . Therefore, a good choice is:
. Therefore, a good choice is:
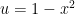
Now, to use the formula we must find and
and  . In this case,
. In this case,
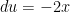 (took the derivative of u)
(took the derivative of u)
Finally, we get
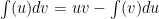
The second integral looks like a simplified version of the one we started with and just like before, integration by parts will allow us to find this integral. If and
and  then:
then:
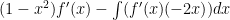
After all of that, this as far as you can go. We don’t know enough about f(x) to know what the last integral is but we were able to take the original integral and simplify it down a bit. As you can see, this involved quite a few steps, so if there is one that doesn’t make sense please feel free to ask!
To apply this, we have to decide what
Now, to use the formula we must find
(took the derivative of dv)
Finally, we get
The second integral looks like a simplified version of the one we started with and just like before, integration by parts will allow us to find this integral. If
(after integration by parts on the integral part)
(distribute the negative)
After all of that, this as far as you can go. We don’t know enough about f(x) to know what the last integral is but we were able to take the original integral and simplify it down a bit. As you can see, this involved quite a few steps, so if there is one that doesn’t make sense please feel free to ask!