Starting this week, we will start posting a calculus problem with its solution (hidden of course!)! Sometimes easy and sometimes hard, these problems could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice!
This week’s problem
Find the integral:
This problem can be done with a straightforward u substitution. If you let  then
then  . Solving for
. Solving for 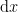 then gives
then gives 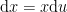 .
.
Therefore, our integral becomes: