Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.
This week’s problem
Find the derivative of
Looking at this function, the first thing you should notice is that it is a product. Yes, there is a composite function ( ) but it is PART OF the product. So your first step should be to use the product rule.
) but it is PART OF the product. So your first step should be to use the product rule.

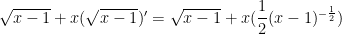
Now the second part involves a derivative of the composite function, so use the chain rule.
At this point, the calculus part is done and it is time to simplify using algebra: