Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.
This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)
Find the integral: .
What I’m hoping catches your eye is the denominator of 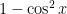 – for two reasons. First of all, with this denominator there, it is unclear how to proceed with the integral. Secondly, you should have the identity
– for two reasons. First of all, with this denominator there, it is unclear how to proceed with the integral. Secondly, you should have the identity
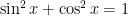
BURNED into your brain! Using this identity, you can rewrite the entire integral.

Now this integral can be found using the substitution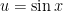 . If
. If 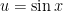 , then
, then 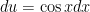 and
and 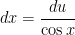 . Then the integral becomes:
. Then the integral becomes:
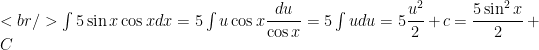
Note: You could have used and your final answer would be
and your final answer would be 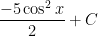 . Now, this does not EQUAL the above answer but they differ only by a constant which is accounted for in C.
. Now, this does not EQUAL the above answer but they differ only by a constant which is accounted for in C.
BURNED into your brain! Using this identity, you can rewrite the entire integral.
Now this integral can be found using the substitution
Note: You could have used