Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.
This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)
The graph of a function 
Think about any parabola (and if you can’t picture one, graph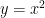 
on your calculator or wolfram alpha to remember!). The vertex of any parabola is basically a turning point. That is, the graph changes from increasing to decreasing and vice-versa.
on your calculator or wolfram alpha to remember!). The vertex of any parabola is basically a turning point. That is, the graph changes from increasing to decreasing and vice-versa.
What does this have to do with derivatives? Well, the derivative at a point where the graph of a continuous function is changing from increasing (where the derivative is positive) to decreasing (where the derivative is negative) will be zero. In this example, since the vertex is at 
