Business Calculus

Calculus Problem of the Week November 4, 2011

Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.

Find the derivative of $f(x)=4(\cos x - \sin x)^2 + 8 \sin x \cos x$ .

See the solution.

While I think random exercises to practice even the “easier” concepts are always a good idea, I did leave a little trick in this one.

Before you take the derivative, see if you can find any way to simplify things to a more useful form. For example, if you expand the squared term :

$f(x)=4(\cos x - \sin x)^2 + 8 \sin x \cos x$
= $f(x)=4(\cos^2 x - 2\sin x \cos x + \sin^2 x) + 8 \sin x \cos x$
= $f(x)= 4( 1 - 2\sin x \cos x) + 8 \sin x \cos x$
= $f(x)= 4( 1 - 2\sin x \cos x) + 8 \sin x \cos x = 4$

Yes this function is just 4, so the derivative is 0. Even if you did this without finding all the terms that cancel, you should have found the same answer here, but it is way more fun to find a shortcut! They aren’t always there but watch for terms that may cancel or simplify before starting any derivative or integral. (ok SOMETIMES this backfires as you need the extra terms, but this is rare!)

Calculus Problem of the Week October 28, 2011

THIS WEEK: Find $f'(0)$ . Hint: This will involve a bit of a “trick” in some sense of the word!

See the solution.

Recall that last week we figured out that $f(0)$ must be zero. Using that, let’s take a look at another way to write the original limit:

$\lim_{x->0}\dfrac{f(x)}{x}=\lim_{x->0}\dfrac{f(x)-f(0)}{x-0}$

Since we know $f(0)=0$ we can rewrite it like this. The question is WHY would we do that? Look really closely. Does that look familiar? What if I changed the x to h? This limit is actually the limit definition of $f'(0)$ ! That means that $f'(0)=4$ since the limit is 4. A little tricky, but it was that step of realizing how to use the results from last week that got us going!

Calculus Problem of the Week October 21, 2011

See the solution.

Think about this for a second: If $f(0)=5$ , $f(0)=100$ , or $f(x)$ as anything other than 0, we wouldn’t be saying the limit is 4.

No, instead, we would be saying the limit doesn’t exist since “plugging in” the zero would give us $\dfrac{0}{0}$ (it is reasonable to assume $\dfrac{f(x)}{x}$ is as simplified as it can be[/latex]).

Therefore, $f(0)=0$ . In this case, finding the limit would involve some kind of algebraic manipulation perhaps that we just can’t see since we don’t know what $f(x)$ is exactly! You can probably think of quite a few functions that would work here like $f(x)=4x$ for example.

Calculus Problem of the Week October 14, 2011

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution. If it doesn’t work, please click the title of this post and then try (I’m working on this!))

Continuing in the direction from last week, this week try to find an example of a function $f(x)$ such that the definite integral from 0 to 1 of $f(x)$ is exactly 1. You should be able to think of at least two different “types” of functions if you want to make it more interesting!
See the solution.

Ok, maybe this is pushing it, but what I am IMAGINING you doing and HOPING you are doing is thinking about what an integral actually is. An integral in this sense is a way of measuring AREA. So really, you are trying to think of a function that would have an area of 1 under it from 0 to 1.

One example of such a function is $f(x)=1$ which is graphed below:

As you can see, from 0 to 1, the area under the curve is the area of the square with sides of length 1 so the area would be 1. This means the integral will be 1 as well and if you check:
$\int_{0}^{1}(1) dx=x|_{0}^{1}=1$

What else? Well, could we get a triangle in that space so that it would have an area of 1? Triangles have area $\dfrac{1}{2}bh$ where b is for base and h is for height. The integral is from 0 to 1 so the base would be 1 – therefore the height would have to be 2 to get an area of 1. Ok, that means it would have to go through the points (0,0) and (1,2) and be a straight line… What function can we get to make that happen?

Aha! $f(x)=2x$ will work! Check the integral like we did above to see.

Calculus Problem of the Week October 7 2011

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution. If it doesn’t work, please click the title of this post and then try (I’m working on this!))

This week, I am going with something other than a mere calculation. Give an example of a function which does not have a derivative of zero at any point in its domain and explain why your function “works” as an example. (There is one type of function that would be the easy example – if you think you figure that out, try to find a different example of another type of function)

See the solution.

As you start to think about this, a natural thought would be “what does it mean for the derivative to be zero at a point?”. There are several possible answers here but one is probably more useful: it means that the tangent line is horizontal.

In other words, this question is asking you to find a function that does not have a horizontal tangent line. The “easier” set of function for which this would be true is the set of linear functions $y=mx+b$ . Unless the slope is zero, $y'=m$ where m is a nonzero number.

What about other examples? If you can find a function where f'(x)=0 has no solutions then you are set! For instance, $\dfrac{1}{x+5}$ which has a derivative of $\dfrac{-1}{(x+5)^2}$ . This derivative is never equal to zero.

Calculus Problem of the Week September 30, 2011

See the solution.

This limit is actually f'(x) for $f(x)=\sqrt{x+1}$ . Recall the definition of the derivative of a function at a point x:

$\lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h}$ . (sometimes delta X is used instead of h)
If you simply try to plug in zero for h, you will get 0/0 which is an indeterminate form. You can think of this as basically giving you now information other than “try another way!”.
One of the “classic” techniques to deal with this is by rationalizing the numerator (or denominator if that is where the “root functions” are) by multiplying it by the conjugate. The conjugate will have the exact same terms but a different sign in the middle. In this instance, the conjugate is $\sqrt{x+1+h}+\sqrt{x+1}$ . Two things to keep in mind:

Anytime you perform an operation like this to a fraction, you must perform it to both the numerator and the denominator. That way, it still has the same value, it just looks different.
Since the conjugate has an opposite sign, you will eliminate all of the terms with roots – which is the whole reason to use it! BUT, you will have these terms appear where they weren’t before. Usually this is OK.

So, multiplying by the conjugate in both the numerator and denominator in this example:
$\lim_{h\to 0}\dfrac{\sqrt{x+1+h}-\sqrt{x+1}}{h} = \lim_{h\to 0}\dfrac{\sqrt{x+1+h}-\sqrt{x+1}}{h} \left(\dfrac{\sqrt{x+1+h}+\sqrt{x+1}}{\sqrt{x+1+h}+\sqrt{x+1}}\right)$
Now, cancel out the h’s and then plug in zero for any remaining h:
$\lim_{h\to 0}\dfrac{(x+h+1)-(x+1)}{h(\sqrt{x+1+h}+\sqrt{x+1})}=\lim_{h\to 0}\dfrac{h}{h(\sqrt{x+1+h}+\sqrt{x+1})}=\lim_{h\to 0}\dfrac{1}{\sqrt{x+1+h}+\sqrt{x+1}}=\dfrac{1}{2\sqrt{x+1}}$ .

Rationalizing the numerator is what allowed me to find this limit “simply” by plugging in the zero. This technique should be one you remember, as it comes up pretty regularly!

Calculus Problem of the Week September 23, 2011

See the solution.

Before you can find the area between the two graphs, you must find where the graphs intersect. These points will be on the boundaries of any region or regions enclosed by the graphs. In order to find where they intersect, you must find where they share the same points – in other words, you must set them equal to each other and solve for x.

$x^4-x^2=x^3$

$x^4-x^3-x^2=0$

$x^2(x^2-x-1)=0$

$x^2=0$ and $x^2-x-1=0$

At this stage we have two equations to solve. The first equation is simple and gives us $x=0$ . But, the second equation isn’t so simple because it doesn’t factor! In order to solve this, you must use the quadratic formula.

$x^2-x-1=0$

$x=\dfrac{-(-1)\pm \sqrt{(-1)^2-4(1)(-1)}}{2(1)}$

$=\dfrac{1\pm \sqrt{5}}{2}$

We have found that there are three points where the graphs intersect: $x=0$ , $x=\dfrac{1+ \sqrt{5}}{2}$ , and $=\dfrac{1 - \sqrt{5}}{2}$ . The second piece of information we need before we can go ahead and find the area enclosed by the two graphs is which function is “larger” in each enclosed region. Really what I’m looking for is which function is higher on the y-axis than the other. By far, the best method to figure this out is to graph both functions.

As you can see above, there are two regions. In the second region, it is clear that $y=x^3$ is the lrager function. But what about the tiny region on the left? Zooming in a bit…

Aha! $y=x^3$ is the larger function in both regions. This means the area enclosed by the two graphs in the left hand region is:

Also, the area enclosed by the right hand region is:

Therefore the total area enclosed by the two graphs is the sum of these two integrals. By far, we have already done the most important part of this. The rest is just calculations and arithmetic and can easily be done by a computer. However, I will show you a little bit of it to show you how far I would go to put this in a calculator. For things like this, doing a little bit of arithmetic before you enter anything into the calculator can make your life much easier.

The first integral:
$0 - \left(\dfrac{(\dfrac{1}{2})^4(1-\sqrt(5))^4}{4}-\dfrac{(\dfrac{1}{2})^5(1-\sqrt(5))^5}{5}+\dfrac{(\dfrac{1}{2})^3(1-\sqrt(5))^3}{3}\right) = -\left(\dfrac{(1-\sqrt(5))^4}{64}-\dfrac{(1-\sqrt(5))^5}{160}+\dfrac{(1-\sqrt(5))^3}{24}\right)$

The second integral:
$\left(\dfrac{(\dfrac{1}{2})^4(1+\sqrt(5))^4}{4}-\dfrac{(\dfrac{1}{2})^5(1+\sqrt(5))^5}{5}+\dfrac{(\dfrac{1}{2})^3(1+\sqrt(5))^3}{3}\right) - 0 = \dfrac{(1+\sqrt(5))^4}{64}-\dfrac{(1+\sqrt(5))^5}{160}+\dfrac{(1+\sqrt(5))^3}{24}$

Your first integral should give you 0.907514 and the second should give you 0.0241808 for a total area of about 0.931695.

Important note:
If you are like me, you like to check your work and one great way is wolfram alpha. But, there is a bug in the output if you put in “area between y=your function and y=your other function. You can read about the bug here: http://community.wolframalpha.com/viewtopic.php?f=32&t=74585. The better way to check your answer is to type “integral (x^3-(x^4-x^2)) dx” and scroll down. It is able to find both of the integrals we have above so that you can check your work.

Calculus Problem of the Week September 16 2011

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)

Find the integral: $\int\dfrac{5\sin^3{x}\cos{x}}{1-\cos^2{x}}dx$ .

See the solution.

What I’m hoping catches your eye is the denominator of $1-\cos^2{x}$ – for two reasons. First of all, with this denominator there, it is unclear how to proceed with the integral. Secondly, you should have the identity

$\sin^2{x}+\cos^2{x}=1$

BURNED into your brain! Using this identity, you can rewrite the entire integral.

$\int\dfrac{5\sin^3{x}\cos{x}}{1-\cos^2{x}}dx=\int\dfrac{5\sin^3{x}\cos{x}}{\sin^2{x}}dx=\int5\sin{x}\cos{x}dx$
Now this integral can be found using the substitution $u=\sin{x}$ . If $u=\sin{x}$ , then $du=\cos{x}dx$ and $dx=\dfrac{du}{\cos{x}}$ . Then the integral becomes:
$<br /> \int5\sin{x}\cos{x}dx=5\int u\cos{x}\dfrac{du}{\cos{x}}=5\int udu=5\dfrac{u^2}{2}+c=\dfrac{5\sin^2{x}}{2}+C$
Note: You could have used $u=cos(x)$ and your final answer would be $\dfrac{-5\cos^2{x}}{2}+C$ . Now, this does not EQUAL the above answer but they differ only by a constant which is accounted for in C.

Calculus Problem of the Week September 9, 2011

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)

Suppose you have an equilateral triangle whose sides are each 6 inches. Let’s say you were to draw a rectangle inside of this triangle such that the base of the rectangle was on the base of the triangle. What is the maximum area your rectangle can have?

See the solution.

The first thing you have to do here is a little bit of a “leap of faith”. In other words, we have to decide where in the triangle the rectangle would have to be in order to get the most area. I think it is obvious (there is the leap of faith!) that it would have to be in the middle. Feel free to argue with me in the comments about this but it is certainly true. Here is my picture:

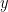
I have decided to call the bottom part of the rectangle $x$ and the longer part $y$ . If we want to maximize area, then we want to maximize $A=xy$ . The problem now becomes: “How do we get this into one variable?”. Once I do this, then I can easily take the derivative and find the maximum value of this area function!

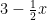
In the picture above, I started thinking about what information I could get out of our original picture. I know each side is 6 inches in length. So, if I drop down from the top of the triangle, I should have length 3 on each side. Also, since the rectangle is in the center, I will have half that length on one side of the line and half on the other. The remaining length would then be $3-\frac{1}{2}x$ . My goal is to write $y$ in terms of $x$ . We are closer to this than you think!

Take a look at the highlighted triangle. That triangle was there the whole time I just added a little information to it. The big piece of information I added is the fact that the angle to the left is 60 degrees. I know this because for any equilateral triangle (triangle with sides that are all the same), the angles are 60 degrees.

The next thing to notice is that the highlighted triangle is a RIGHT triangle. This means that I can use a trig function to determine sides. In fact, I can say that:

$\tan(60 deg)=\dfrac{y}{3-\frac{1}{2}x}$ .
Remember 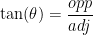$\tan(\theta)=\dfrac{opp}{adj}$
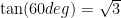
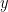
Since $\tan(60 deg)=\sqrt{3}$ , I can solve for $y$ and get:
$y=\sqrt{3}(3-\frac{1}{2}x)$
Plugging this back into area:
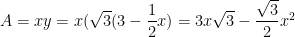
$A=xy=x(\sqrt{3}(3-\dfrac{1}{2}x)=3x\sqrt{3}-\dfrac{\sqrt{3}}{2}x^2$

Finally, to find the maximum area I will take the derivative of this function, find when its derivative is zero, and finally plug that value back into the area function.
Finding the derivative:

$A'=3\sqrt{3}-\sqrt{3}x$

Finding when the derivative is zero:

$3\sqrt{3}-x\sqrt{3}=0$
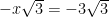
$-x\sqrt{3}=-3\sqrt{3}$
$x=3$

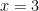
Using the value of x to find the maximum area:

$A=3x\sqrt{3}-\dfrac{\sqrt{3}}{2}x^2$

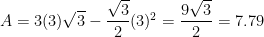$A=3(3)\sqrt{3}-\dfrac{\sqrt{3}}{2}(3)^2 = \dfrac{9\sqrt{3}}{2} = 7.79$ square inches.

Calculus Problem of the Week September 2, 2011

This week’s problem was inspired by something mentioned on twitter and while it is not a difficult derivative, thinking about using the “not obvious” rule will help you look at functions in a new and different way. Try it out!
This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)

Find the derivative of $f(x)=e^{x+5}$ using the product rule.

See the solution.

The “obvious” way to approach this would be with the chain rule but to make this work with the product rule, you have to go back and remember the laws of exponents.

You can rewrite $e^{x+5}$ as $(e^x)(e^5)$ . Normally, you would be totally right in saying “well, why would you do THAT?! You just made it more complicated!” but I was trying to find a way to write it as a product in order to use the product rule. Once you have rewritten it this way:

$[(e^x)(e^5)]'=(e^x)'(e^5)+(e^x)(e^5)'=(e^x)(e^5)+(e^x)(0)=(e^x)(e^5)=e^{x+5}$ .
(I used the fact that $e^5$ is a constant so its derivative is zero)

Based on this, $e^{x+5}$ is its own derivative which makes sense since the slope of the “inside” function is 1.