Business Calculus

Calculus Problem of the Week August 26, 2011

Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)

The graph of a function f(x) is a parabola with a vertex at (2,3). Find f'(2).

See the solution.

Think about any parabola (and if you can’t picture one, graph y=x^2 on your calculator or wolfram alpha to remember!). The vertex of any parabola is basically a turning point. That is, the graph changes from increasing to decreasing and vice-versa.

What does this have to do with derivatives? Well, the derivative at a point where the graph of a continuous function is changing from increasing (where the derivative is positive) to decreasing (where the derivative is negative) will be zero. In this example, since the vertex is at x=2, f'(2)=0.

Calculus Video: Remember Your Derivative Rules (this time with the help of Ceelo’s “Forget you.”)

The trend continues where I am just hanging out on twitter, seeing what is going on and what happens? Across my feed comes a mention of a math song. I swear I won’t click it but just like before, I do and end up having to share. It looks like I’m just a sucker for these things.

You’ll find the star of this video is the chain rule, but there are others if you watch carefully!

Via Sweeny Math

Calculus Problem of the Week August 19, 2011

Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)
Find the integral (as far as you can): \int(1-x^2)f''(x)dx. Assume that f is a function such that the derivatives and integral are well defined.

See the solution.

A first thought may be to distribute the f''(x), but after that step it is unclear how to proceed! Instead, notice that we have a product of two functions, namely (1-x^2) and f''(x). This is a good indication that integration by parts would be a helpful approach!
\int(u) dv=uv-\int(v)du

To apply this, we have to decide what u and dv are. Clearly if we take the derivative of f(x) again we will be moving in the wrong direction by making things more complicated. Also, it is really easy to take the derivative of 1-x^2 which we will have to do with whatever we choose as u. Therefore, a good choice is:

u=1-x^2

dv=f''(x)


Now, to use the formula we must find du and v. In this case,

du=-2x (took the derivative of u)

v=f'(x) (took the derivative of dv)


Finally, we get
\int(u) dv=uv-\int(v)du

=(1-x^2)f'(x)-\int(f'(x)(-2x))dx


The second integral looks like a simplified version of the one we started with and just like before, integration by parts will allow us to find this integral. If u=-2x and dv=f'(x) then:

(1-x^2)f'(x)-\int(f'(x)(-2x))dx

=(1-x^2)f'(x)-(-2xf(x)-\int(-2f(x))dx) (after integration by parts on the integral part)

=(1-x^2)f'(x)+2xf(x)-2\int(f(x))dx (distribute the negative)


After all of that, this as far as you can go. We don’t know enough about f(x) to know what the last integral is but we were able to take the original integral and simplify it down a bit. As you can see, this involved quite a few steps, so if there is one that doesn’t make sense please feel free to ask!

Calculus Problem of the Week August 12, 2011

Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)
Find the integral: \int(\tan(x)\tan(2x)\tan(3x))dx. Hint: \tan(3x)=\tan(2x+x).

See the solution.

I gave you the hint above to try to get you to think about using some identities here as trying this integral directly could be insane!

Using the identity for sums of Tangent, we know that \tan(3x)=\tan(2x+x)=\dfrac{\tan(2x)+\tan(x)}{1-\tan(x)\tan(2x)}. But, if you simply replace the term in the integral with this, you are STILL making things more complicated than they need be. Let’s take a closer look at this identity and see what other information is in it.


\tan(3x)=\dfrac{\tan(2x)+\tan(x)}{1-\tan(x)\tan(2x)}

If we cross multiply:

\tan(3x)(1-\tan(x)\tan(2x))=\tan(2x)+\tan(x)

then distribute:

\tan(3x)-\tan(x)\tan(2x)\tan(3x)=\tan(2x)+\tan(x)


Aha – do you see that our integral is right in there? If you solve for \tan(x)\tan(2x)\tan(3x) in this identity then you find that \tan(x)\tan(2x)\tan(3x)=\tan(3x)-\tan(2x)-\tan(x). Why is this such a big deal? It looks really similar to what we had before right? Well, you can’t just take the integral of individual terms when they are multiplied but you can if the terms are added or subtracted. In other words this means that:

\int(\tan(x)\tan(2x)\tan(3x))dx=\int(\tan(3x)-\tan(2x)-\tan(x))dx
=\int(\tan(3x))dx-\int(\tan(2x))dx-\int(\tan(x))dx

Now you can use u substitution (u=3x,2x respectively) and the fact that \int(\tan(x))=-\ln|\cos(x)| to find the integral.

\int(\tan(x)\tan(2x)\tan(3x))dx=\int(\tan(3x)-tan(2x)-tan(x))dx
=-\dfrac{1}{3}\ln|\cos(3x)|+\dfrac{1}{2}\ln|\cos(2x)|-\ln|\cos(x)|+C

Calculus Problem of the Week – August 5, 2011

Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.

If you have noticed the date changes lately, I have shifted these from being posted on Monday’s to being posted on Fridays to fit better with when I want to post other types of articles. You will still find the problem right here every week though!

Although I usually don’t like them, this week I have decided to go with a bit of a “trick” question. (I was inspired by some AP questions I saw recently, but this is good no matter what level you are studying at)

This is only a trick question in the sense that if you don’t immediately recognize one important feature, you will probably get it wrong or at the very least do much more work than necessary. If you DO notice it, you will find this is a very routine problem. Hmmm have I now ruined it? Take a look and see how you do.

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)
Find the derivative of e^3cos(x)

See the solution.

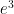
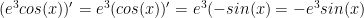
You may be tempted to start off with the product rule here, but that would actually be overkill (it WILL work if you do it right). Instead, notice that e^3 is a constant. Therefore, (e^3cos(x))'=e^3(cos(x))'=e^3(-sin(x)=-e^3sin(x).

As you can see, very routine – pay close attention in calculus to things that LOOK like variables but are actually constants to save yourself from getting the problem wrong or more work than necessary.

Calculus Problem of the Week – Week of July 25, 2011

Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)
Suppose you know the following information about two functions:

f(2)=1
g(2)=2
f'(2)=7
g'(2)=-3

Use this information to find [f(g(2))]'.

See the solution.

f(g(x)) is a composite function, so to find the derivative you should use the chain rule. Applying the chain rule here would give us [f(g(x))]'=f'(g(x))\cdot g'(x). Therefore [f(g(2))]'=f'(g(2))\cdot g'(2)=f'(2)g'(2)=7\cdot (-3)=-21

Notice that if it wasn’t true that g(2)=2, we wouldn’t have been able to do this since we only knew f(2).

Calculus Problem of the Week July 18, 2011

Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)
The function f is a continuous function whose second derivative is a non-zero constant and the equation of the tangent line to f at x=2 is y=12x-12. If the function f itself is not a constant and has only one term, find f.
See the solution.

There is a lot of information about f given in the problem, so a good first step is to try to pull even more information out. Lets look at each statement:

  • The function f is a continuous function whose second derivative is a non-zero constant

    • This means that if we take the derivative twice we end up with a number like 5 or -2. What functions give us a constant other than zero when we take their derivative? LINEAR FUNCTIONS. So, the first derivative must be linear! Ok we are making progress. Now, what type of function gives you a linear function when you take the derivative? A QUADRATIC like ax^2+bx+c.

  • The equation of the tangent line to f at x=2 is y=12x-12

    • This means that f'(2)=12

  • The function f itself is not a constant and has only one term

    • We already figured out that f would look something like ax^2+bx+c since it must be quadratic. But, if it only one term that means that f=ax^2 for some number a that is not zero. We already know that f'(2)=12 so I will find the derivative of our f so far: f'=(ax^2)'=2ax. Finally since this must be 12 when x=2, 4a=12 and therefore a=3 giving us f=3x^2

Calculus Problem of the Week July 11 2011

Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)
This week we will go with a “routine” limit problem that highlights an aspect of limits people tend to forget!
Without using a graph, find the limit: \lim_{x->-1}\dfrac{x^2+3x+2}{x+1}

See the solution.

The “rule” I have for finding limits is to plug the number in unless something “breaks”. That is, plug the number in and see if I end up with a 0/0. If you try to plug in -1 in this case, you get \dfrac{(-1)^2+3(-1)+2}{-1+1}=\dfrac{0}{0}. Many people at this stage would assume that the limit doesn’t exist, BUT THAT ISN’T NECESSARILY TRUE! 0/0 is an indeterminate form and getting it is a sign that you need to try another approach.

Luckily, the function we have simplifies nicely: \dfrac{x^2+3x+2}{x+1}=\dfrac{(x+1)(x+2)}{x+1}=x+2. This means that \lim_{x->-1}\dfrac{x^2+3x+2}{x+1}=\lim_{x->-1}(x+2)=-1+2=1.

Calculus Problem of the Week July 4, 2011

Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.

This week’s problem
Find the derivative of \dfrac{x^4}{x} using THREE DIFFERENT METHODS.
See the solution.

It may seem strange to find this derivative in three different ways, but it allows you to practice thinking about problems differently. If you can recognize different ways to approach a given problem, you can more easily decide which is the best. (it also gives you a chance to really practice your algebra skills!)

I will go through three of the more “obvious” approaches. If you found another way – please post!

Method 1: Simplify first.

Using the laws of exponents, \dfrac{x^4}{x}=x^3. Therefore the derivative is 3x^2 (by the power rule)

Method 2: The quotient rule.

(\dfrac{x^4}{x})'=\dfrac{(x^4)'(x)-(x^4)(x)'}{x^2}=\dfrac{(4x^3)(x)-x^4}{x^2}=\dfrac{4x^4-x^4}{x^2}=\dfrac{3x^4}{x^2}=3x^2. It wasn’t pretty but it worked!

Method 3: The product rule.

First rewrite \dfrac{x^4}{x} as a product: (x^4)(x^{-1}). Now:

((x^4)(x^{-1}))'=(x^4)'(x^{-1})+(x^4)(x^-1)'=(4x^3)(x^{-1})+(x^4)(-x^{-2})=\dfrac{4x^3}{x}-\dfrac{x^4}{x^2}=4x^2-x^2=3x^2.

PS you may have noticed that I used a slightly different way of writing out the product and quotient rules. While it is equivalent to the form you find in textbooks, I have always found this way easier to remember for myself and students!